株ログは複数の企業と提携しており、当サイトを経由して商品を購入することで、売り上げの一部が還元されることがあります。しかしながら当サイトのランキング等の評価については提携の有無や支払いの有無が影響していることはありません。
- 本記事の内容
- 『2020年9月実施』FP3級実技試験の過去問の解説です。
【日本FP協会】
Q.17
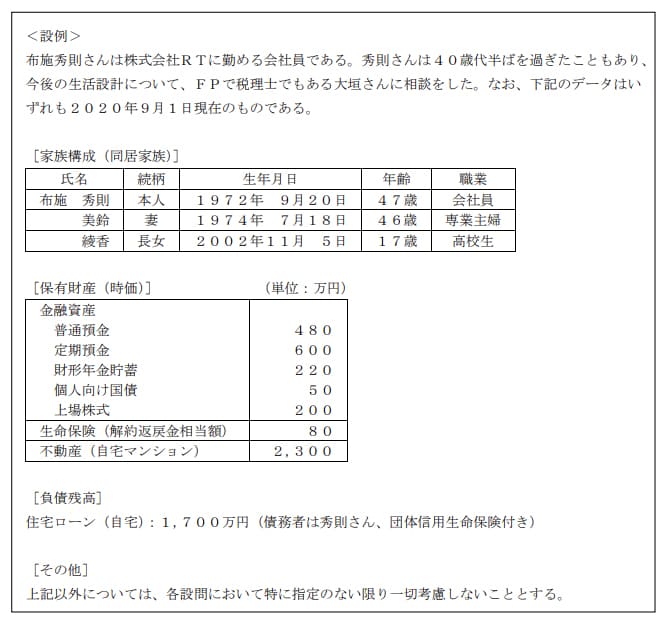
先に下記の資料をご覧ください。(Q16.17.18.19.20で使います)
秀則さんは、今後15年間で毎年36万円ずつ積立貯蓄をして、老後の資金準備をしたいと考えている。積立期間中に年利2.0%で複利運用できるものとした場合、15年後の積立金額として、正しいものはどれか。なお、下記<資料>の3つの係数の中から最も適切な係数を選択して計算し、解答に当たっては、千円未満を四捨五入すること。また、税金や記載のない事項については一切考慮しないこととする。
- 7,268,000円
- 6,225,000円
- 4,626,000円
2が適切
6,225,000円が適切です。
今回のポイントは下記です。
- 使う係数は年金終価係数
- 係数が全く分からない場合
順に見ていきましょう。
- 使う係数は減債基金係数
『積立』というキーワードが出てきた場合は次のどちらかを使います。
- キーワード『積立』
- 減債基金係数→毎年の積立額はいくらか?(げんざい)
年金終価係数→積み立て後の金額はいくらか?(しょうらい)
将来の事について聞かれているので、今回は年金終価係数を使用します。
よって計算式は下記になります。
360,000×17.293=6,225,480≒6,225,000

michi
6つの係数は
- げんさいききんけいすう→げんざい
- ねんきんしゅうかけいすう→しょうらい
このように『げ』と『し』が現在、将来にそれぞれ対応しています。
他の係数も似たような感じで覚えられます。
- 係数が全く分からない場合
設問から分かることは下記です。
- 15万円を36年間積み立てる
ここから15万円×36年=540万円とアタリを付けます。
この場合近い数値は下記です。
| 年金終価係数 | 36万円×17.293≒6,225,000円 |
| 年金現価係数 | 36万円×12.849≒4,626,000円 |
上記の表から分かるように、年金現価係数ではお金が減ってしまっているのでおかしいことが分かります。
よって条件に合うのは年金終価係数となります。