株ログは複数の企業と提携しており、当サイトを経由して商品を購入することで、売り上げの一部が還元されることがあります。しかしながら当サイトのランキング等の評価については提携の有無や支払いの有無が影響していることはありません。
本記事の内容
『2020年9月実施』FP3級試験学科試験の過去問の解説です。
【日本FP協会】【きんざい】共通
Q.31
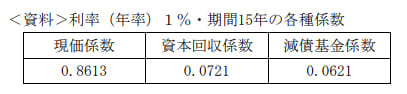
900万円を準備するために、15年間、毎年均等に積み立て、利率(年率)1%で複利運用する場合、必要となる毎年の積立金額は、下記の<資料>の係数を使用して算出すると( )である。
1) 516,780円
2) 558,900円
3) 600,000円
2が適切
本設問のポイントは2つです。
- 使用する係数は減債基金係数
- 係数が分からなくてもオッケー
【ポイント1】
『積立』というワードが出てきたら下記のどちらかです。
- 将来受け取る金額を求めるなら→年金終価係数
- 現在いくら必要かを求めるなら→減債基金係数
よって減債基金係数を使います。
【ポイント2】
この手の計算問題は係数の意味が分からなくても正答できます。
今回はそれぞれの係数を計算すると558,900円しか出てきません(笑)
- 9,000,000×0.8613=7,751,700(現価係数)
- 9,000,000×0.0721=648,900(資本回収係数)
- 9,000,000×0.0621=558,900(減債基金係数)
ありがちなのが表の1番右にあるので、3と答えてしまうことです。
焦らずにゆっくりやってくださいね。
 michi
michi
キーワード『まとまったお金』
- 現価係数→現在いくら必要か?(げんざい)
- 終価係数→将来いくらになるか?(しょうらい)
キーワード『積立』
- 減債基金係数→毎年の積立額はいくらか?(げんざい)
- 年金終価係数→積み立て後の金額はいくらか?(しょうらい)
キーワード『年金』『返済』
- 年金現価係数→現在いくらの元本が必要か?(げんざい)
- 資本回収係数→将来いくら受け取れるか?(しょうらい)
げんざいの値を求める係数は必ず『げ』が付いて、しょうらいの値を求める係数は必ず『し』が付くので、それで覚えてました(笑)
 michi
michi